Overview

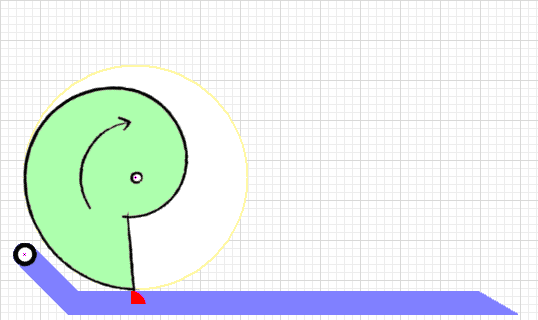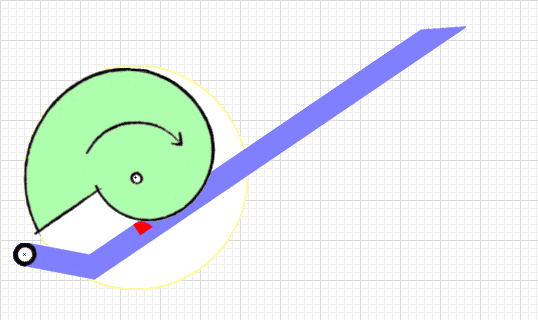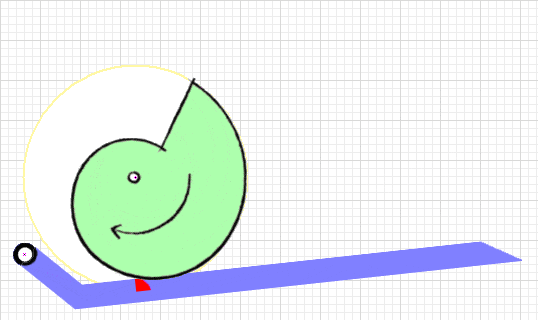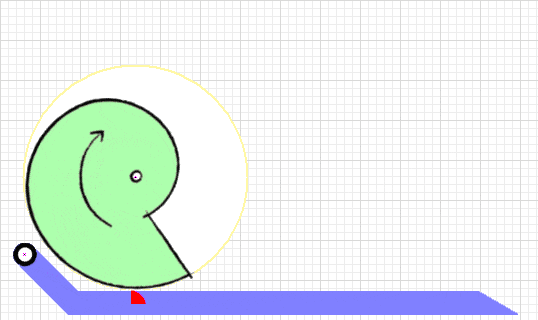The deceptively simple 'Snail Cam' mechanism has seen limited use in robot combat to date, and rarely outside the insect weight classes.

Advantages A properly designed snail cam will keep the torque load on the gearmotor constant thruout the reset cycle, resulting in a quicker reset time with less motor effort. The 'ready' point is a stable flat or detent on the cam that requires no motor torque to hold in place. The snail cam itself can be crafted from plastic using standard shop tools.

Disadvantages Sliding friction between the cam and cam follower can be considerable. Crafting the cam from a low-friction plastic like UHMW polyethylene will keep this manageable, and a needle bearing cam follower can completely eliminate the problem.

Resources Dale Hetherington's detailed build log for antweight 'Dead Air' fills in a lot of detail on design and constuction.

Videos

This spring flipper mechanism from 'M & J Robotics' is a trial-and-error design. The builder says, "The cam shape is just something we adjusted till it worked."

You can hear the motor bog down under torque peaks as it winds the spring. It works, but it wastes a lot of the power and speed available from the motor.

Video

'Jännä' is a 450 gram antweight robot by European YouTuber 'mikromekaanikko'.

The snail cam is well designed and operates at close to optimum performance. This compact and efficient mechanism wouild be a good starting point for your own flipper.

Video

Cam Profile

Using a simple Archimedean spiral cam profile will place a constantly increasing load on the motor powering the cam and cause it to slow as the cam reaches the final stages of spring loading. Gearing the cam motor to meet the high torque needed at the end of the load cycle slows the early part of the cam rotation, resulting in a slower than optimal reset time.

The ideal profile for the 'snail cam' is a parabolic spiral that reduces the lift rate to match the increasing load imposed by the spring as it is extended. This profile keeps the motor speed constant for the entire cycle, resulting in improved cycle time and less strain on the cam motor.

A mathematically perfect parabolic spiral is unfortunately poorly suited for use as a mechanical cam: the vertical drop immediately followed by a precipitous rise is neigh impossible for a mechanical cam follower to negotiate. The exact modifications to the profile will depend on the design of your mechanism. 'Jännä' has a lever-style follower and its cam is modified with a broad flat region pointing toward the lever hinge to provide a suitable landing for the follower and a rapid initial lift.

It's important to get the shape of the parabolic spiral correct to even out the torque load on the motor. The spring becomes harder to compress as it compresses farther, so the cam has to provide a lot of compression at the start of rotation (50% the total is in the first 25% of rotation) and taper to less compression as the load increases (the last 12.5% takes the final 25% of rotation).

The formula for the parabolic spiral in polar coordinates is: Radius = k · θ ^0.5 + minimum cam radius where 'θ' is angular rotation and 'k' is a growth variable that defines the lift of the cam; a 'k' of 0.0527 will give one unit of lift over 360 degrees of rotation. Here's an example for a small snail cam with a 5mm minimum radius and 15mm total lift:

I've created a 'Google Sheets' spreadsheet that will calculate and draw a snail cam profile similar to the pics below. The link requires you to sign-in to your Google account, then offers you a copy of the sheet: Snail Cam Sheet

Spring Force Requirement

Note If the spring 'pre-loads' the snail cam with some force at the minimum lift starting position, the parabolic spiral formula must change in order to keep the torque load on the cam motor constant. The Snail Cam Sheet will make the appropriate change based on the figures you supply for spring force on the cam at the start and end of the lift.

Torque Requirement

In our case the work is the extension of the spring, which takes place over the course of one revolution of the axle. The spring extension force is a linear function (Hooke's law), so we can calculate the average force required to extend the spring as follows:

That plugs into the basic linear work equation [Work = Force * Distance] like this:

Getting close now. One full rotation is 2𝜋 radians, so with a little algebra the rotational work formula transposes to our needed torque equation:

There are some losses due to angular inefficiencies and rubbing friction with the cam, and you will want the motor to deliver the required torque with enough speed to extend the spring quickly. I'd suggest a gearmotor with a stall torque about three times the formula result to avoid bogging and let the motor operate up near its power output peak.

If you don't care to do the math to calculate the torque requirement for your snail cam motor, the same 'Google Sheets' spreadsheet mentioned in the 'Cam Profile' section above does that calculation for you. Here's the link again: Snail Cam Sheet

Motor Control

When you turn off the windshield wipers on an automobile have you noticed how they continue for the rest of the wipe stroke and then stop in the park position? That's what you're looking for and here's how you do it:

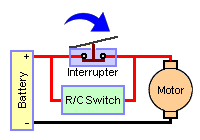
Note A micro switch is simple, but you can certainly use other sensor types: infrared emitter/detector, inductive proximity, magnetic... whatever you're comfortable using.

To see the most recent questions or to ask a new question, go to the