
Privacy Policy

Some of the most common questions submitted to 'Ask Aaron' are about the design of spinning weapons for combat robots. I've edited together Q&A from our archives into a FAQ that should answer the most common inquiries on this topic. More detailed information on weapon design can be found in the Robot Weapons archive.
Spinning weapons are flywheels. They rely on rotational inertia to collect energy from a continuous power source (electric motor, internal combustion engine...) over time and store it as rotational kinetic energy. On impact, the flywheel releases the stored energy in a blow that far exceeds the energy directly available from the continuous source.
Energy Storage
Q: How much energy should my spinning weapon store?
A: Rule-of-thumb: a useful spinning weapon will store at very least 60 joules of energy per kilo of the bot's weightclass -- that comes to about 30 joules per pound. A more typical weapon will store about twice that value. So, a spinning weapon on a robot in the 60 kilo weight class will need to store a minimum of 60 × 60 = 3600 joules of energy, but would be better with three times that much.
 Q: The power of robot rotary weapons is measured in joules, but joules doesn't mean much to me in real world terms. Can you give me an example of a 1000 joule impact with everyday objects?
Q: The power of robot rotary weapons is measured in joules, but joules doesn't mean much to me in real world terms. Can you give me an example of a 1000 joule impact with everyday objects?
A: Sure. A baseball bat hitting a major league home run is an impact of just about 1000 joules. Bear that in mind when you're designing and building your robot -- can you hit it as hard as you can with a baseball bat and have it bounce back for more?
Q: How do I calculate the kinetic energy storage capacity of a spinning weapon?
A: The Combat Robot Design Tools page has links to our Spinner Weapon Calculators:
- Our 'Spinner Weapon Excel Spreadsheet' will calculate the stored kinetic energy, weapon mass, moment of inertia, tip speed, spin-up time, current draw, and the approximate battery capacity requirement for a spinner weapon.
- If you prefer an on-line calculator our 'Javascript Spinner Weapon Calculator' will provide most of the same capability, but with reduced graphic capability.
Q: What type of spinning weapon has the best energy storage -- bar, disk, eggbeater or drum?
Energy storage at 2000 RPM: 710 joules
Energy storage at 2000 RPM: 970 joules
Energy storage at 2000 RPM: 1230 joules
Energy storage at 2000 RPM: 1460 joules
 A: An ideal combat robot spinning weapon places as much mass as far away from the rotational axis as possible to obtain maximum energy storage from the mass. For a given mass and diameter, a drum is better than an eggbeater, an eggbeater is better than a disk, and a disk is better than a bar. Examples:
A: An ideal combat robot spinning weapon places as much mass as far away from the rotational axis as possible to obtain maximum energy storage from the mass. For a given mass and diameter, a drum is better than an eggbeater, an eggbeater is better than a disk, and a disk is better than a bar. Examples:
Rotational Speed
Q: What RPM is best for my spinner weapon?
A: It's certainly tempting to spin a weapon up to stupid fast revs. Kinetic energy increases with the square of speed, so if you double the speed you get four times the energy storage. Awesome!
The problem is that the faster the weapon spins, the harder it is to get the weapon to 'bite' into your opponent and get a powerful hit. A weapon without bite will just skitter across a smooth surface and do no harm at all. If you have no bite you must rely on your opponent to make the mistake of offering a sharp edge to give your weapon something to grab.
How fast is too fast? Section 6.3 in the RioBotz Combat Tutorial has a good explanation of weapon speed and bite, as well as the formulas for calculating bite depth. It's well worth a read. It turns out that the answer depends on the spacing of the impactor teeth and how fast your 'bot moves forward during an attack. You can effectively use greater RPM if you have a single counterweighted impactor and a high rate of closure on your opponent at impact. Decent bite can be very hard to obtain if you have multiple impactors and a timid attack.
Q: How do I calculate 'bite'?
A: Bite is the maximum depth of opponent insertion into the arc of a spinning weapon at a given weapon RPM and forward attack speed. You'll get that maximum bite rarely, just like 13 black only comes around rarely on a roulette wheel. Sometimes your luck will be very poor and you'll hit your opponent just as an impactor tooth is facing them and get no bite at all! On average, you'll get half the max bite -- less as your attack speed drops.
What's the diffference between a little bite and a lot of bite? More match wins! Bite is good, and more bite is better.
I've written a JavaScript 'Bite Calculator' to make it simple for builders to calculate their weapon bite. Fill in the
Q: Is there a calculator to find the right balance of bite and speed for a spinning weapon?
A: There is no single 'right balance' of bite and speed for a given weapon. The balance is situational:
- Fighting a hard-surfaced opponent with no sharp edges calls for all the bite you can muster.
- A drum head-to-head against another drum requires maximum speed and can dispense with bite.
- Small arenas and close fighting call for big bite, while larger arenas and higher closing speeds need less.
- When your opponent has only soft exposed surfaces it may be better to ignore 'bite' and switch to sharp 'shred'.
- If you have a ramp to help your vertical spinner get a shot at your opponent's sharp front under-edge you need very little bite.
Q: How quickly should my weapon spin-up to speed?
A: How much time you have for your spinner to come up to speed depends in large part on the size of the arena. You need to have enough energy stored in your weapon to fend off an opponent who sprints across the arena in an attempt to ram you before your weapon becomes dangerous. In a small arena that doesn't give you much time -- but in a large arena you have an extra couple of beats. It also helps if your robot is nimble enough to dodge a fast ramming attack.
Rule-of-thumb: aim to spin your weapon up to at least 45 joules per kilo of the bot's weight class in the first two seconds.
Motor Selection
Q: What motor do I need to spin up a 4 kg disk to 2000 RPM?
A: Motor selection depends on more than the mass of the weapon. The 'Moment of Inertia' (MOI) of the weapon determines the power needed to spin the weapon up to a given speed in a specified period of time (see: 'How do I calculate the kinetic energy storage capacity of a spinning weapon?' - above). The power needed to spin a solid 4 kg disc to 2000 RPM depends on:
- The diameter of the disc; and
- How quickly you want the disc to reach 2000 RPM.
Examples (calculated by the Team Run Amok Excel Spinner Spreadsheet):
- A 'Small Johnson' motor with 0.56 N-m stall torque and a no-load 24,000 RPM speed geared down 12:1 will spin this disc up to 1300 RPM (420 joules) in about 1.4 seconds and will approach 2000 RPM (970 joules) in about 4.3 seconds. Not bad.
An aluminum disk 600mm diameter and 5mm thick also weighs 4 kg. It will store about 3850 joules of rotational energy at 2000 RPM.
- That same 'Small Johnson' motor geared down 12:1 will spin this disc up to 1300 RPM (1700 joules) in about 5.8 seconds and will approach 2000 RPM (3850 joules) in about 17.8 seconds. That's too long to wait for spin-up.
- A more powerful Ampflow E30-150 motor with 5.0 N-m stall torque and a no-load 5700 RPM speed geared down 2.85:1 will spin this disc up to 1300 RPM (1700 joules) in about 2.8 seconds and will reach 2000 RPM (3850 joules) in about 8.4 seconds. A bit slow for some arenas, but a good balance between spin-up time and energy storage.
Q: I want to use a brushless motor for my spinner weapon. How do I calculate the 'Stall Torque' of a brushless motor to enter into the on-line Spinner Weapon Kinetic Energy Calculator?
The 'Help File' for the Spinner Weapon Kinetic Energy Calculator includes a simple javascript calculator that will give a stall torque estimate suitable for the calculator -- I've copied it below for your convenience. The Kv (RPM per volt) and Ri (internal resistance) values are commonly given in brushless motor specs. A more comprehensive and accurate model of 'soft start' spinner weapon performance is available from the Team Run Amok Brushless Spinner Excel Spreadsheet.
The calculated estimate is useful for weapon spin-up calculations, but a brushless motor torque curve is non-linear and 'stall' torque is not the torque peak as it is in brushed motors. Use of this torque estimate for drivetrain calculations is highly questionable.
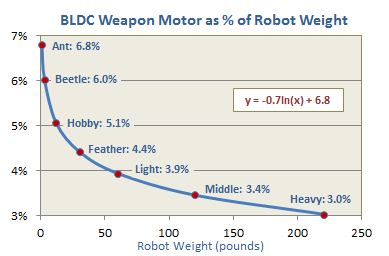
A: Specifics will depend on your design, but popular beetleweight spinner weapon motors run about 150 watts per pound of robot and about 6% of the total robot weight. For a beetle, that typically translates to outrunner motors in 28mm or 36mm diameters.
Q: Weapon BLDC motor: 6% of total mass; this rule applicable to FW and LW weight classes? [Paris, France]
A: The guideline (not a rule) was specific for beetleweights, and extrapolating to larger robots is non-linear. The Square-Cube Law requires larger robots to devote a greater percentage of their mass to structural elements, leaving less for other components. As robot weight increases you find proportionally smaller spinner motors and those motors are pumping out less power per unit weight because they are also subject to square-cube issues for structure and heat dissipation. A heavyweight spinner motor might typically produce 50 watts per pound of robot at about 3% of the robot mass. Fitting this to a log curve gives the chart shown -- but it's only a guideline.
Current successful beetle spinners have brushless weapon motors that cluster around 6% of the robot weight -- but you can't run that backwards to say that any motor that is 6% of robot weight will make a good beetle spinner motor. Different BLDC motor versions of the same size and mass will have quite different performance figures. Combined with the '150 watts per pound' guideline it's a quick check to see if you're in the ballpark. If you're considering a beetle weapon motor that weighs 3% or 12% of your total weight allowance you'll want to make sure you have good reason to use it.
The motor is rated for a maximum of 90 amps, or 2000 watts. My ESC claims it can supply 200 amps. I am using A123 cells which claim 50 amps constant and a 10 second peak of 120 amps.
My question is... how do I get the spreadsheet to limit the current used by the weapon motor? I can play with the numbers and adjust the value for Ri. A value of 150 uses a maximum of 112 amps, but I'm not sure that will give me correct numbers for spin up either. This has a 4.3 second spin up, but it only uses the 112 amps for a brief moment which is likely not correct.
Based on this, it seems the correct spin up time is somewhere between 0.4 and 4.3 seconds. Is there a way to narrow it down further? [Kansas/Missouri Border]
A: [Mark J.] The spreadsheet assumes that the internal resistance of the motor is the only resistance in the system, but the motor controller and battery also have internal resistances. These additional resistances become increasingly important as the resistance of the motor itself decreases -- and the 0.014 ohm resistance of your selected motor is pretty damned small. Let's add in an estimate for those other resistances.
Plugging that figure into the spreadsheet for the Ri produces a spinup time of 2.5 seconds with a current peak at 180 amps -- pushing above 120 amps for about 0.25 second. I think your weapon system will be fine.
A: Any time you apply a force to change the direction that the axis of a spinning mass is pointing, gyroscopic resistance will attempt to redirect that force at a right angle. This may have undesireable effects on robot mobility.
A: T.i. Combat Robotics put together a great tutorial on Designing Around the Gyroscopic Effect . They step thru all the math and discuss adjustments to specific design elements that can tame weapon gyro forces. The page includes a javascript 'Gyroscopic Effect Calculator' for quickly checking and adjusting proposed designs. The solution may be as simple as limiting the robot turn rate with transmitter programming.
Design Considerations
A: The maximum useable impactor height is calculated by a simple formula, but figuring out the correct values to enter can be tricky:
The 'Attack Speed' is the closing rate between your robot and your target and it's target. Given that attacks with both robots charging directly toward each other at full speed are uncommon, the value is usually assumed to be your own robot's top speed. In small arenas with cautious competitors the attack speed may be considerably less. Best judgement applies here.
Example: a robot with a top speed of 5 MPH (88 inches per second) has a weapon with two impact teeth spinning at 5300 RPM.
A more complete explanation of tooth height and 'bite' is featured in section Section 6.3 of the RioBotz Combat Tutorial.
The "S-Hook" is meant for countering horizontals; less material to get caught by their blade.
I think the real standout here is the "Reaper" assuming it's strong enough to survive, but the big MoI for the "Pendulum" is hard to ignore.
What do you think?
 Q: About how large a brushless motor do I need for a beetle spinner weapon? [Cincinnati, Ohio]
Q: About how large a brushless motor do I need for a beetle spinner weapon? [Cincinnati, Ohio]
Q: I'm trying to use your Spinner Weapon Spreadsheet but I think I'm missing an important detail. Based on the numbers it seems my little motor is going to melt into oblivion as it draws considerably more current than it can handle.
That will give a total resistance of your motor/controller/battery around
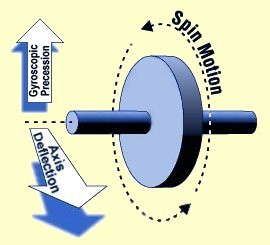 Q: I know any robot with a spinning weapon is subject to gyroscopic forces, but how does this differ for vertical and horizontal spinners?
Q: I know any robot with a spinning weapon is subject to gyroscopic forces, but how does this differ for vertical and horizontal spinners?
Q: I've seen vertical spinner 'bots that looked very similar to each other but one had HUGE problems with gyroscopic forces and one didn't. How do I make sure my design isn't going to have trouble?
Q: How tall should the impact teeth on my drum (or disk) spinner be?
Useable Impactor Height = (Attack speed [in units per second] × 60) ÷ (Weapon RPM × Number of Impactors)
Useable Impactor Height = (88 inches per second × 60) ÷ (5300 RPM × 2 Impactors)
= 5280 ÷ 10,600 = real close to 0.5 inch
Q: I couldn't decide on a vertival weapon blade for my 1-pound ant, so I made five. All of these blades have a 72mm cut diameter, and are 0.250" AR500 steel:

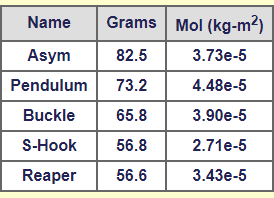
A: I think you're underestimating the impact of spinning the asymetric blade "twice as fast to make up for it". Rotational energy storage increases with the square of speed so twice as fast equals four times the energy storage -- that's an exponential increase in weapon power. The Run Amok Spinner Weapon Kinetic Energy Calculator gives these kinetic energy storage figures for each of your blades spinning at 8000 RPM:
| Name | Energy @ 8K | Joules/Gram |
|---|---|---|
| Asym | 13 joules | 0.16 |
| Pendulum | 16 joules | 0.22 |
| Buckle | 14 joules | 0.21 |
| S-Hook | 10 joules | 0.18 |
| Reaper | 12 joules | 0.21 |
In this comparison 'Asym' doesn't look like a great option, but taking advantage of the added bite 'Asym' has (What's bite?) and spinning it faster has dramatic results:
- Spinning 'Asym' 50% faster to 12,000 RPM increases energy storage to 30 joules and yields 33% better bite than the dual impactor bars have at 8000 RPM. That's 0.36 joules per gram of bar weight.
- Spinning 'Asym' 100% faster to 16,000 RPM increases energy storage to 53 joules and maintains the same bite the dual impactor bars have at 8000 RPM. That's 0.64 joules per gram of bar weight.
Q: My robot design calls for a drum weapon 15 cm long with a weight of 7 kg. What drum diameter and wall thickness will store maximum energy?
A: Spend some time studying up on flywheel physics. It's more than I can cover here, but essentially: the farther mass is placed from the axis of rotation, the greater the rotational energy storage an object will have.
The variables that determine the energy that a spinning drum holds at a given RPM are: mass, material density, diameter, and length. Given those variables you can calculate the required wall thickness. You've specified mass and length, and I'll assume that you're using steel. Holding mass, length, and speed constant the rotational energy storage will increase with increasing diameter.
Examples - for a bare steel tube 15 cm long (no end caps or impactors):
- 15 cm diameter - 14 mm thickness - mass is 7 kg and at 4000 RPM it stores 2900 joules of energy
- 20 cm diameter - 10 mm thickness - mass is 7 kg and at 4000 RPM it stores 5600 joules of energy
- 25 cm diameter - 8 mm thickness - mass is 7 kg and at 4000 RPM it stores 9200 joules of energy
Q: I want to build a drum weapon that stores 5000 joules of energy at 5000 RPM. Mass is limited to 13 kg and diameter cannot exceed 15 cm. What should be the drum's diameter and wall thickness?
A: Stored energy in a cylinder rotating around its radius center is a function of:
- Rotational Speed (RPM)
- Material Density
- Drum Diameter
- Drum Length
- Drum Mass
You've given me a desired output and only three of the five variables (rotational speed, maximim mass, and diameter). By selecting values for material density and drum length, I can give a design solution for any wall thickness to meet your criteria. For example:
- A steel cylinder 15 cm in diameter 100 mm in length, and solid to the center will weigh 11.5 kilos and will store 5000 joules of energy at 5000 RPM.
- A steel cylinder 15 cm in diameter 300 mm in length, with a 6.7 mm thick wall will weigh 7.1 kilos and will store 5000 joules of energy at 5000 RPM.
- An aluminum cylinder 15 cm in diameter 300 mm in length, with a 31 mm thick wall will weigh 9.6 kilos and will store 5000 joules at 5000 RPM.
- An aluminum cylinder 15 cm in diameter 2600 mm in length, with a 2 mm thick wall will weigh 6.7 kilos and will store 5000 joules at 5000 RPM.
It's quite odd to specify a weapon diameter, speed, and energy storage as starting parameters and back into the other dimensions. In particular, specifying such a high rotational speed is detrimental to the overall performance of a spinner weapon. Were it my weapon, I would design it to achieve the desired energy storage at the slowest possible speed -- something like:
- A steel cylinder 15 cm in diameter 380 mm in length, with a 10 mm thick wall will weigh 13 kilos and will store 5000 joules at 3760 RPM.
A 5000 joule weapon does you no good at all if it's spinning too fast to have decent 'bite' and the ability to transfer that energy to your opponent in a single, huge impact. Slow it down a bit. A larger diameter drum would be able to store the same energy at an even slower speed -- example:
- A steel cylinder 20 cm in diameter 390 mm in length, with a 7 mm thick wall will weigh 13 kilos and will store 5000 joules of energy at 2780 RPM.
Or even better:
- A steel cylinder 25 cm in diameter 360 mm in length, with a 6 mm thick wall will weigh 13 kilos and will store 5000 joules of energy at 2175 RPM.
Don't compromise weapon performance with dimensional restrictions that you can avoid, and design for the lowest weapon speed that will store enough energy to be effective.
 Q: Spinning weapons are always rated by how much kinetic energy they store (joules), but doesn't momentum also matter? If you have two spinners with the same kinetic energy storage how does momentum effect their destructive potential?
Q: Spinning weapons are always rated by how much kinetic energy they store (joules), but doesn't momentum also matter? If you have two spinners with the same kinetic energy storage how does momentum effect their destructive potential?
A: Mark J. Momentum does have an effect on destructive potential, but you may be surprised by what that effect turns out to be.
Here are the equations for Kinetic Energy and Momentum:
Momentum = Mass × Velocity
Being struck by the runaway frozen turkey will attempt to accelerate you (and the chair) to ten miles-per-hour, but conservation of momentum will reduce the final speed of the combined turkey/skateboard/human/chair mass. Because of the higher approach speed the turkey will exert the accelerating force (kinetic energy) over a shorter period of time and, because the definition of power is work per unit time, the impact will be greater. Could leave a nasty bruise.
Getting hit by a 100+ MPH baseball is just plain ugly. The ball will attempt to transfer its entire accelerative force in a blink, resulting in a great deal of force exerted in a small impact area. We're talking potential broken bones and knocking the you/chair straight over. The full energy will be absorbed at the impact site and will not be dissipated over significant time and distance. This is a trip to the emergency room.
A Reality Check
If you're not winning matches it isn't because you have a poor weapon.

Copyright 2015 by Mark Joerger -- all rights reserved.










